Tổng hợp công thức Toán ôn thi vào lớp 10 phần Lý thuyết đường thẳng song song và đường thẳng cắt nhau
Lý thuyết tổng hợp công thức Toán ôn thi vào lớp 10 phần Lý thuyết đường thẳng song song và đường thẳng cắt nhau được chia sẻ trong bài viết dưới đây gồm các phần kiến thức trọng tâm nhất. Hy vọng sẽ giúp các bạn học sinh dễ dàng tiếp thu và nắm vững kiến thức môn Toán lớp 9 để ôn thi vào lớp 10 đạt kết quả cao nhất nhé!
LÝ THUYẾT VỀ ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU
Cách xác định hai đường thẳng song song, cắt nhau, vuông góc
1. Cho hai đường thẳng (d1 ): y = ax + b (a ≠ 0)
(d2 ): y =a’x + b’ (a’ ≠ 0)
+ (d1 ) // (d2 ) ⇔ a = a’; b ≠ b’
+ (d1 ) ≡ (d2 ) ⇔ a = a’; b = b’
+ (d1 ) cắt (d2 ) ⇔ a ≠ a’
2. Khi a > 0 thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn;
Khi a < 0 thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù.
3. Bổ sung
Cho hai đường thẳng (d1 ): y = ax + b (a ≠ 0)
(d2 ): y = a’x + b’ (a’ ≠ 0)
+ (d1 ) ⊥ (d2 ) ⇔ a.a’ = 1
+ Nếu (d1 ) cắt (d2 ) thì hoành độ giao điểm là nghiệm của phương trình
ax + b = a’x + b’ (gọi là phương trình hoành độ giao điểm)
+ Góc α là góc tạo bởi đường thẳng y = ax + b và trục Ox. Nếu a > 0 thì tanα = a
Phương pháp giải
Cho hai đường thẳng:
(d1 ): y = ax + b (a ≠ 0)
(d2 ): y = a’x + b’ (a’ ≠ 0)
+ (d1 ) // (d2 ) ⇔ a = a’; b ≠ b’
+ (d1 ) ≡ (d2 ) ⇔ a = a’; b = b’
+ (d1 ) cắt (d2 ) ⇔ a ≠ a’
+ d1 ⊥ d2 ⇔ a.a’ = -1.
Ví dụ minh họa
Ví dụ 1: Hãy chỉ ra các cặp đường thẳng song song và vuông góc trong các đường thẳng sau:
d1: y = 2x + 3

d4: y = 0,5x – 3
d5: y = 5 + 2x
d6: 7 – 2x
Hướng dẫn:
Hai cặp đường thẳng song song là:
d1 // d5 vì a = a’ = 2; b ≠ b’ (3 ≠ 5)
d2 // d4 vì a = a’ = 0,5; b ≠ b’ (2 ≠ -3)
Bốn cặp đường thẳng vuông góc với nhau là: d1 ⊥ d3; d2 ⊥ d6; d3 ⊥ d5; d4 ⊥ d6 vì đều có a.a’ = -1.
Ví dụ 2: Chứng tỏ rằng hai đường thẳng sau luôn cắt nhau với mọi giá trị của m
a) (d1 ): y = (m2 – 4m + 5)x + 1 và (d1 ): y = (-x + m)/2
b) (d3 ): y = (m2 + 1)x + 2018 và (d4 ): y = -mx + 2012
Hướng dẫn:
a) Xét (d1 ) có a = m2 – 4m + 5 = (m – 2)2 + 1 > 0
(d2 ) có a’ = (-1)/2 < 0
⇒ a ≠ a’ với mọi m nên (d1 ) luôn cắt (d2 )
b) Xét (d3 ) có a = m2 + 1
(d4 ) có a’ = -m
Ta có: a – a’ = m2 + 1 + m = (m + 1/2)2 + 3/4 > 0 ∀m
⇒ a ≠ a’ với mọi m nên (d3 ) luôn cắt (d4 )
Bài tập vận dụng
Bài 1: Tìm ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong số các đường thẳng sau:
a) y = √3x – 1 (1) b) y = 2 – x (2)
c) y = -0,3x (3) d) y = -0,3x – 1 (4)
e) y = 3 + √3x (5) f) y = -x + 3 (6)
Bài 2: Cho hai hàm số bậc nhất y = 2x + 3k và y = (2m + 1)x + 2k – 3
Tìm điều kiện đối với m và k để đồ thị của hai hàm số là:
a) Hai đường thẳng cắt nhau
b) Hai đường thẳng song song
c) Hai đường thẳng trùng nhau.
Hướng dẫn giải và đáp án
Bài 1:
Các cặp đường thẳng cắt nhau là: (1) và (2); (1) và (3); (1) và (4)
Các cặp đường thẳng song song là: 1) và (5); (2) và (6); (3) và (4)
Bài 2:
y = 2x + 3k và y = (2m + 1)x + 2k – 3
a) Hai đường thẳng trên cắt nhau
⇔ 2m + 1 ≠ 2 ⇔ m ≠ 1/2
b) Hai đường thẳng trên song song với nhau

c) Hai đường thẳng trên trùng nhau
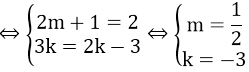
Cách viết phương trình đường thẳng song song với đường thẳng
Phương pháp giải
Viết phương trình đường thẳng đi qua một điểm và song song với một đường thẳng cho trước: Gọi phương trình đường thẳng cần tìm là y = ax + b.
+ Sử dụng điều kiện hai đường thẳng song song với nhau để xác định hệ số a.
+ Với a tìm được, sử dụng điều kiện còn lại để xác định tung độ gốc b
Ví dụ minh họa
Ví dụ 1:
Cho 2 đường thẳng (d1 ): y = (2 – m2 )x – m – 5 (d2 ): y = -2x + 2m + 1
Tìm m để hai đường thẳng song song với nhau
Hướng dẫn:
(d1) // (d2)
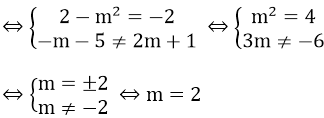
Vậy với m = 2 thì hai đường thẳng trên song song với nhau.
Ví dụ 2: Cho đường thẳng (d): 2x + y – 3 = 0 và điểm M (-1; 1). Viết phương trình đường thẳng (d’) đi qua điểm M và song song với (d).
Hướng dẫn:
Gọi phương trình đường thẳng (d’) là y = ax + b
Ta có: (d): 2x + y – 3 = 0 hay y = -2x + 3.
Vì (d) // (d’) nên a = -2 và b ≠ 3.
Mặt khác, (d’) đi qua điểm M (-1; 1) nên 1 = a.(-1) + b ⇔ -a + b = 1
⇔ -(-2) + b = 1 ⇔ b = -1 (≠ 3).
Vậy phương trình đường thẳng cần tìm là y = -2x – 1.
Bài tập vận dụng
Bài 1: Viết phương trình đường thẳng (d) đi qua điểm (-3; 4) và song song với đường thẳng (d’): y = 2x – 1
Bài 2: Cho M (0; 2), N(1; 0), P(-1; -1) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Viết phương trình đường thẳng AB.
Hướng dẫn giải và đáp án
Bài 1:
Gọi phương trình đường thẳng (d) là y = ax + b
Do (d) // (d’) nên a = 2; b ≠ -1.
(d) đi qua điểm (-3; 4) nên: 4 = -3.a + b ⇔ 4 = -3.2 + b ⇔ b = 10.
Vậy phương trình đường thẳng cần tìm là y = 2x + 10.
Bài 2:
Gọi phương trình đường thẳng MN là: y = ax + b. Ta có:
N(1; 0) ∈ MN ⇒ 0 = a.1 + b ⇔ a = -b
M(0; 2) ∈ MN ⇒ 2 = a.0 + b ⇔ b = 2 ⇒ a = -2.
Vậy phương trình đường thẳng MN là y = – 2x + 2.
Vì M, N lần lượt là trung điểm của CB và CA nên MN là đường trung bình của tam giác ABC ⇒ MN // AB
Vì AB // MN nên phương trình đường thẳng AB có dạng: y = -2x + b’ (b’ ≠ 2)
Vì P (-1; -1) là trung điểm của đoạn thẳng AB nên đường thẳng AB đi qua P.
⇒ -1 = -2.(-1) + b’ ⇒ b’ = -3 (thỏa mãn)
Vậy phương trình đường thẳng AB là y = -2x – 3.

Cách Viết phương trình đường thẳng vuông góc với đường thẳng
Phương pháp giải
Viết phương trình đường thẳng đi qua một điểm và vuông góc với một đường thẳng cho trước:
Gọi phương trình đường thẳng cần tìm là y = ax + b.
+ Sử dụng điều kiện hai đường thẳng vuông góc để xác định hệ số a.
+ Với a tìm được, sử dụng điều kiện điểm thuộc đường thẳng để xác định tung độ gốc b.
Ví dụ minh họa
Ví dụ 1: Tìm m để đường thẳng (d): y = m2 x + 1 – m vuông góc với đường thẳng (d’): y = (-1)/4 x + 2018
Hướng dẫn:
(d) ⊥ (d’) ⇔ a.a’ = -1 ⇔ m2.((-1)/4) = -1 ⇔ m2 = 4 ⇔ m = ±2.
Vậy với m = ±2 thì (d) ⊥ (d’)
Ví dụ 2: Viết phương trình đường thẳng (d1) đi qua điểm A (-2; 3) và vuông góc với (d2):y = -2x + 2m + 1
Hướng dẫn:
Gọi phương trình đường thẳng (d1) là y = ax + b.
(d1) ⊥ (d2) ⇔ a.a’ = -1 ⇔ a.(-2) = -1 ⇔ a = 1/2
Khi đó, phương trình đường thẳng (d1) có dạng y = 1/2.x + b
Do (d1) đi qua điểm A (-2; 3) nên tọa độ điểm A thỏa mãn phương trình (d1)
⇒ 3 = 1/2.(-2) + b ⇒ b = 4
Vậy phương trình đường thẳng (d1) là y = 1/2.x + 4
Bài tập vận dụng
Bài 1: Tìm a và b, biết đường thẳng (d1):y = ax + b vuông góc với đường thẳng (d2) y = (-1)/4.x và (d1) đi qua điểm P (-2; 3)
Bài 2: Cho ba điểm A(1; 2), B(3; 0), C(0; 1)
a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác
b) Viết phương trình đường thẳng chứa đường cao AH của ΔABC
Hướng dẫn giải và đáp án

Bài 1:
(d1 ) ⊥ (d2) ⇔ a.a’ = -1 ⇔ a.((-1)/4) = -1 ⇔ a = 4
Khi đó, phương trình đường thẳng (d1) có dạng: y = 4x + b
Do (d1 ) đi qua điểm P (-2; 3) nên tọa độ điểm P thỏa mãn phương trình (d1)
3 = 4.(-2) + b ⇔ b = -11.
Vậy phương trình đường thẳng cần tìm là y = 4x – 11.
Bài 2:
a) Gọi phương trình đường thẳng đi qua B(3; 0), C(0; 1) là BC: y = ax + b
Ta có: B ∈ BC nên 0 = a.3 + b ⇔ b + 3a = 0
C ∈ BC nên 1 = a.0 + b ⇔ b = 1
⇒ 3a + 1 = 0 ⇒ a = (-1)/3
Phương trình đường thẳng BC là y = (-1)/3.x + 1
Thay tọa độ điểm A vào phương trình đường thẳng BC không thỏa mãn nên A ∉ BC hay A, B,C không thẳng hàng.
Vậy 3 điểm A, B, C là ba đỉnh của một tam giác.
b) Gọi phương trình đường cao AH là (d’): y = a’ x + b’
Do AH là đường cao của tam giác ABC nên:
AH ⊥ BC ⇔ (d’) ⊥ BC ⇔ a.a’ = -1
⇔ a’.(-1)/3 = -1 ⇔ a’ = 3
⇒ y = 3x + b’
Mặt khác A(1; 2) ∈ (d’) nên: 2 = 3.1 + b’ ⇒ b’ = -1
Vậy phương trình đường cao AH là y = 3x – 1
Trên đây là tổng hợp lý thuyết về công thức Toán ôn thi vào lớp 10 phần lý thuyết đường thẳng song song và đường thẳng cắt nhau. Phần tổng hợp này sẽ giúp các bạn tóm gọn kiến thức một cách nhanh chóng và biết cách vận dụng vào bài tập nhanh hơn. Chúc các bạn học tốt!




